Accelerated Expansion and the ZPF From A Modification To M-Theory
By: Paul Karl Hoiland
If one follows the implications of this theory then one is led to the conclusion that the Zero Point Field( the Vacuum) must be a real entity. This is founded upon the following. A 1D harmonic oscillator has states, which can be raised or lowered. This is done in units of N of Planks constant divided by 2Pi times frequency. In terms of momentum P and position Q, the Hamiltonian of the system becomes H=(p**+w**g**)/2. This added to the excitation states have energies acceptable in QM calculations for N Greater than or equal to zero. However, if the kinetic energy or temperature is lowered to zero Kelvin there remains a zero point energy still equal to planks constant/2. If one sums that over frequency a large energy density remains.
Now acceleration through this ZPF causes a particle to acquire inertial mass due to drag no matter what the direction of that motion because the field is uniform in all directions. Also, according to what we have thus established, and in agreement with formula put forth by Duthoff, Haisch, and Rueda in their equations for the ZDF, the ZDF does not gravitate in and of itself. In our theory the energies are such that either field without the other would not gravitate. In fact, even combined both space-time fields have negative and positive values that cancel to the 120th place. This is why the actual experienced ZPF remains low on a global scale. But, it would still produce an EM drag that effects charged particles undergoing acceleration through it.
If one treats the inertial rest mass of a particle as a coordinate in a dimensionally extended space-time then there remains two choices which are mathematically equivelent. These are the gravitational and particle units. When this is applied to a fully-covariant, dimensionally extended theory such as mine that is based upon Riemannian Geometry, these choices transform to coordinate frames.
In this current approach the normal Einstein Field Equations are replaced with a 10D field equation and the vacuum Tensor=o. The equations can then be broken into sets. The first is just regular GR with matter derived from them by virtue of an extra metric coefficient and derivative with respect to the extra coordinates. The second set becomes Maxwell's equation for EM. The next is a conservative equation for the scalar field in the extended metric. The finial ones having to do with the symmetry operations of SU(3), SU(2), U(1) from QED and QCD but here united and incorporated with gravity into one field theory.
What keeps space-time flat and still able to accelerate its expansion rate on an observational level is the energy stored in 6D Higg's Space-time from Inflation.
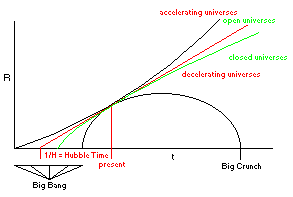
Below is a diagram of normal Big Bang based space-time curvatures that are possible. With this model it is possible for Space-time to evolve through all of these stages.
Two other papers derived from this theory are below the log section.
Preservation of SR and GR under this Theory.
The general theory of relativity is founded on a set of field-equations, formulated by Albert Einstein in 1915, which deal with the gravitational force-field. The bold idea of Einstein was to regard the gravitational force as a property of space-time. Thus, General Relativity is essentially a geometrization of gravitation and its language is the mathematics of differential 4-dimensional geometry - three dimensions for space and one for time. General Relativity saw its advent as an extension of Special Relativity, also owed to Einstein, which is based on the following two assumptions: (an inertial system is a frame of reference in which the velocity of a body is constant unless it is influenced by forces)
The laws of physics are the same in all inertial systems and no preferred inertial system exists.
The speed of light in free space is the same in all inertial systems.
Now, since recent observations have found reason to think that the Fine Structure Constant varies over time this would at first imply that the second and first assumptions are incorrect. Indead, no matter how they try to reword it the first would be incorrect since a constant those laws are based upon would be changing. However, this theory does allow for what would appear to be a changing constant without that constant actually changing. If the Space-time field itself as relates to global curvature is allowed to evolve over time then one can have a constant that stays the same, but would have redshift effects simular to those noted in recent experiments. As, the global curvature changed and the overall mass density changed the stretching of the space-time manifold would account for all shifting. Thus, this theory keeps the first assumption as true.
The second assumption can be proved only under a changing constant idea if one limits the inertial system in question to one from the specific time frame being studied. As far as other time frames are concerned it would become false when two seperate history frames where compared. Under this proposed theory, there is no change in the actual constant. Thus, in all inertia frames it remains true.
First and Second Laws of Thermodynamics Perserved by this Modification.
By: Paul Karl Hoiland
Ludwig Boltzmann [1] was the first to model the realm of possibilities as ordered and disordered states in the development of the second law of thermodynamics. To explain entropy, Boltzmann generally concluded that the disorder of a closed system increases, because of an imbalance between ordered and disordered states. He reasoned that there is naturally a greater quantity of disordered states compared to ordered states.
Boltzmann also generally envisioned that an axis exists between order and disorder. In one direction along that axis, the number of ordered states decreases toward a state of highest order. In the other direction, the number of disordered states increases notably with some ambiguity. If we assume an aggregate perspective of Boltzmann's model, we can generally identify a wedge shape, closing at the end of highest possible order, where we must presume a single extreme state, while in the other direction there is an endless and indefinite expansion of increasingly disordered states, apparently without end.
Once Boltzmann introduced the second law, others assumed this same conceptualization of order, and came to accept this wedge like model of all possible states as a general description of nature, perhaps without any of the usual scrutiny a fundamental image of nature requires if it is to be maintained. The model has been maintained peaceably, mainly because there has been no challenges and also because the vaguely understood probabilities of such a model have seemed previously to agree with the cosmological behavior of time and the process of microsystems reaching equilibrium.
This system allows for a evolving curvature of space-time and its expansion rate without any violation to these laws. It does so because, not only is the 4D space-time subject to them. But, the actual process whereby the 6D space-time releases its energy stored from inflation is of its very nature due to entropy. The system is simply seeking its lowest energy state which demands the most disordered state and along the other axis the most ordered being a return to its spinless, energyless state.
Why The Cosmological Constant must vary.
By: Paul Karl Hoiland
In 1916, Albert Einstein made up his General Theory of Relativity without thinking of a cosmological constant. The view of that time was that the Universe had to be static. Yet, when he tried to model such an universe, he realized he cannot do it unless either he considers a negative pressure of matter (which is a totally unreasonable hypothesis) or he introduces a term (which he called cosmological constant), acting like a repulsive gravitational force. Later, after Hubble and others had discovered the Universe wasn’t static, but expanding Einstein dropped it. More recent observations that have found evidence that the expansion rate changes with time and some of the work with String Theory have caused that term, sometimes referred to as Omega to resurface. But, most people, unless they are cosmologists, physicists, or Astronomers have no idea what this is all about. I will now try to explain the math of it and why based upon two items I feel it varies over time.
The magnitude of the negative pressure needed for energy conservation is easily found to
be P = -u = -rho*c2 where P is the pressure, u is the vacuum energy density, and rho is the
equivalent mass density using E = m*c2.
But in General Relativity, pressure has weight, which means that the gravitational
acceleration at the edge of a uniform density sphere is not given by
g = GM/R2 = (4*pi/3)*G*rho*R
but is rather given by
g = (4*pi/3)*G*(rho+3P/c2)*R
Now Einstein wanted a static model, which means that g = 0, but he also wanted to
have some matter, so rho > 0, and thus he needed P < 0. In fact, by setting
rho(vacuum) = 0.5*rho(matter)
he had a total density of 1.5*rho(matter) and a total pressure of -0.5*rho(matter)*c2 since the
pressure from ordinary matter is essentially zero (compared to rho*c2). Thus rho+3P/c2 = 0
and the gravitational acceleration was zero,
g = (4*pi/3)*G*(rho(matter)-2*rho(vacuum))*R = 0
allowing a static Universe.
The basic flaw in Einstein’s original model is that it is unstable. Its akin to a pencel
ballanced on its point. Soon or later it will fall one way or another. When one considers the
results from QM predictions one finds the following. The equations of quantum field theory
describing interacting particles and anti-particles of mass M are very hard to solve exactly. With
a large amount of mathematical work it is possible to prove that the ground state of this system
has an energy that is less than infinity. But there is no obvious reason why the energy of this
ground state should be zero. One expects roughly one particle in every volume equal to the
Compton wavelength of the particle cubed, which gives a vacuum density of
rho(vacuum) = M4c3/h3 = 1013 [M/proton mass]4 gm/cc
For the highest reasonable elementary particle mass, the Planck mass of 20 micrograms, this
density is more than 1091 gm/cc. So there must be a suppression mechanism at work now that
reduces the vacuum energy density by at least 120 orders of magnitude.
As I have already laid out in the modification to M-Theory paper, this mechanism is found in the structure of 6D Higgs space-time. But what I have not done is actual show these as it
directly relates to the cosmological constant.
If the supernova data and the CMB data are correct, then the vacuum density is about
75% of the total density now. But at redshift z=2, which occurred 11 Gyr ago for this model if
Ho = 65, the vacuum energy density was only 10% of the total density. And 11 Gyr in the future
the vacuum density will be 96% of the total density. If one compares this locally within our
solar system where we know the masses involved and the distances on finds the following.
a = R*(2*pi/P)2
which has to be equal to the gravitational acceleration worked out above:
a = R*(2*pi/P)2 = g = GM(Sun)/R2 - (8*pi/3)*G*rho(vacuum))*R
If rho(vacuum) = 0 then we get
(4*pi2/GM)*R3 = P2
which is Kepler's Third Law. But if the vacuum density is not zero, then one gets a fractional
change in period of
dP/P = (4*pi/3)*R3*rho(vacuum)/M(sun) = rho(vacuum)/rho(bar)
where the average density inside radius R is rho(bar) = M/((4*pi/3)*R3). This can only be
checked for planets where we have an independent measurement of the distance from the Sun.
The Voyager spacecraft allowed very precise distances to Uranus and Neptune to be
determined, and Anderson et al. (1995, ApJ, 448, 885) found that dP/P = (1+/-1) parts per
million at Neptune's distance from the Sun. This gives us a Solar System limit of
rho(vacuum) = (5+/-5)*10-18 < 2*10-17 gm/cc. From this we can begin to
figure out how much it varies due to the seperation distance between any
large body of mass. The cosmological constant will also cause a precession of the perihelion of a planet. Recent data from Mars via the landers and other such mission has
produced a value of rho(vacuum) < 2*10-19 gm/cc. It is this last value I believe is most
accurate at this time. I believe that more precise data will show that the value of both Omega
and rhu varies not only with time. But also with the amount of mass density in any given region
of space. I base this not only upon theory, but
also upon the fact that, even though at large distances one does get a certain error. That
error factor can not be that large. From this
I do find evidence then that has been showing
us for some time that it does evolve with time.
MORE PROOF AGAINST THE AETHER THEORY
Item taken from a book on old Aether Theory.
Speed of Light in A Clear Dense Medium
It is well known that light travels slower in a clear medium such as glass and that light will regain its speed instantaneously when it re-emerges from the glass. The existing wave and particle theories of quantum mechanics cannot explain these observations completely. If light travels slower in glass because it goes through the absorption and emission processes, it should be completely scattered when it enters the glass, and that was not the case. If light really traveled slower in glass, then the problems arise when we try to visualize the processes by which light regains its speed instantaneously as it re-emerges from the glass. Model Mechanics resolves these problems automatically. The processes involved can be visualized as follows: The glass is in constant motions in the E-MATRIX. These motions curved the E-STRINGS within the glass and when light enters the glass, it is being transmitted by the curved E-STRINGS and thus, it appears to travel slower. When light re-emerges from the glass, it is being transmitted by normal E-STRINGS (not curved) and thus, it appears that light regains its speed instantaneously.
The answer to this is simple. First off, it is both QM and modern field theory that has led to this being turned around the other direction and used to speed up light in certain accelerating mediums. Secondly, as has already been established in this theory, since Omega varies according to the density of matter in a local area. Any solid substance, such as a glass, since its matter density is higher should show a slowing of light as it passes through that medium.
Those who subscribe to the Aether Theory usually put forth that the original double slit experiments do not prove QM. The results were simply accountable to movements of the slits. The problem I find with this is that given the size of a photon as compared to the distance between those slits, that movement would have been such that the whole lab had to be shaking. The problem I find with this is that hiding ones head in the sand and blaming everything under the sun for your problems does not deal with the real life facts. Face up to the truth. The old Aether theory is without substance. What they also tend to forget is that, while a material Aether was done away with. The Space-time SR and GR brought us a newer and richer form of Aether. Only this one is composed of fields with the substance being what those fields, under certain conditions, form.
A Minimal Time Slice
If one is going to use, as, Physicists have recently postulated a "time quantum", a
minimum time interval, then that interval must be very small indeed. But, it would have to
be also large enough to encompass the smallest particle. That being the graviton. Thus, as the
basic tube of string was found to be vibrating in different energy states it would simply be a
reflection of an increased tension of those lattice intervals or an increase of stretch of there
structure. If, one takes the measurement of the speed of light as 186300 MPS and divides it by
2^59th one gets a size of 9.315^-55 meters for a basic unit. The reason I choice this has to do
with the kinetic energy of a graviton as the basic unit in relation to the speed of light. It seemed
at least a starting point. Now, if you divide the weak photon by the graviton one gets 1^34.
This times 9.315^-55 gives you 9.315^-21. That divided by the 9.315^-55 equals the 1^34.
This translated into an event description says that our original graviton has undergone a
minimal time interval change of 1^34th power. A Gluon following this logic would have
undergone a 1.01001^39th power interval change. All other particles then become a division
of it downwards back to the graviton. Now if C, as an interval of time, equals a time interval of
2^59th basic units. Then a relation of mass to time interval can be established as such.
If one applies this time interval to the Lorentz formula one finds that the Time Interval
shrinks as an object or particle are accelerated. This translates to a smaller measuring factor
the faster an object moves. Thus, mass will increase.
Thus, there is no problem with the idea some have proposed of establishing a time
quanta. In fact, it does establish time as a dimension on equal footing with the other
dimensions. One thing time has always lacked is a universal reference point. But lets
explore and see what having a universal time reference will do to some other equations.
If we apply the Lorentz formula to two separate events one finds that relativity still
remains valid. There will be a time difference between a stationary observer and those
of an object moving relative to that stationary point of reference. The only difference
now is one has a means of universally establishing time anywhere within the universe.
The time difference is as follows. As velocity goes up the time interval increases. This
is why mass goes up. What has happened is the time interval has expanded due to drag
against the energy of 6D space-time. This is understood as different from what clock
time does because the time interval is tied to mass. The point of this whole exercise has been
to show that there is an energy to the vacuum and that energy effects the fields of our space-
time via a drag effect as an object is accelerated. It is this drag effect that is responsible
for inertia. What this drag does is it expands the time interval in the opposite direction to
that of acceleration. Which accounts for why the length of an object under acceleration
shrinks the faster an object goes. It also shows that the energy of 6D space-time
stays the same. What has changed is the energy of 4D space-time.
Another application of this minimal time slice is in the area of Blackholes. If there is
a smallest unit of time, and a smallest field element in the since of a String. Then it
follows that there is a limit to which gravity can compact space-time. That limit would
as such avoid the actual singularity issue. This does not in any fashion take away from
the idea of gravity in a local region of space being able to produce a region that light
itself cannot escape from. Nor does it effect in any way the proposed theory recently
backed up by String Theory that Blackholes do radiate energy back into space-time.
What must be remembered is our Strings are not solid objects in the since of the old
Newtonian or Atom concept. They are interwoven fields that form space-time. It is
their localized energy within a given area that we define as a particle. Not some solid hard
substance. The part that is being defined in this case is the smallest amount of that energy
that can exist due to the fact that our Strings have a certain smallest vibrational state which
has been defined as a graviton. This is well in keeping with regular QM.
Indead, one aspect of QM and the evolution of the Cosmos that has always been
ignored is that given the almost universally accepted concept of Inflation. There is a point
at which under QM no smaller unit as relates to time can be utilized than that which exists at
the border between expansion and inflation. This is because the energies involved in the
process of Inflation have a negative quality to them. Even if one could get beyond that point
the amount of energy needed by any process to work further backwards goes off the scale.
This has been echoed by many when they speak of the infinities that crop up at the Plank
scale. But few have ever looked at its implication as relates to Blackhole structure. If
infinites crop up at the Plank scale which is far larger than any normal concept of a singular
point. Than nothing can ever reach that singularity point unless one choices to redefine that point by the Plank scale limit.
|