But even inspite of String Theory solving a lot of problems(ie. Entrophy of Blackholes) it still in its current form commonly called M-Theory for Membrane or Magic has many problems of its own. String Theory from it's start has always been based upon another theory called SuperSymetry. With SUSY type theories all matter particles have their counter-part in force carriers. The idea being that Fermions can transform into Bosons and back. The problem is that nature,as we know it, has no observational evidence for the Supersymetry partiners.
Another problem to some people is the added extra dimensions. These again have no direct observational evidence in nature.
The Theory that I am about to propose is a modification to M-Theory that explains the problem of SUSY and those hidden dimensions. For the most part it is basic M-Theory. But its starting point is different.
Before I continue with my discussion of this modified M-Theory it is best to lay some basic ground work.
The original field theories of the Standard Model pictured particles as points in space-time. There are two standard field theory models, which while giveing accurate data on the particles, has several problems inherent within. The first of these is Quantum Chromodynamics. This is the theory that describes the Strong Force carrier. The second is Quantum Electrodynamics. This deals with the combined electromagnetic and weak forces.
The problem with these theories is that not only have the two never been acurately combined, they both exclude General Relativity from their fold. Thus, at best, they are incomplete.
String Theory replaces the point particle with something that does not inscribe a point and as such avoids the singularity problem that normally generates infinities as an answer. Also, instead of a long list of different particles one has different particles as manifestations of the same basic string vibrating in different modes. String Theory is also the only theory where General Relativity not only can be combined with it. In fact, the basic fundamental state of the String is the Spin-2 carrier of gravity, the Graviton. |
Simulation Of Compaction.
|
My newest article on The Mysteries of Space-Time
Try Galatic surf for a Galaxy of fun.
As has already been mentioned, to have a chance of being realistic, the six extra space dimensions must curl up into a tiny geometrical space, whose size should be comparable to the string length Lst..
Since space-time geometry is determined dynamically (as in general relativity), only geometries that satisfy the dynamical equations are allowed.
The HE string theory, compactified on a particular kind of six-dimensional space, called a Calabi--Yau manifold, has many qualitative features at low energies that resemble the standard model. In particular, the low mass fermions (identified as quarks and leptons) occur in families, whose number is controlled by the topology of the CY manifold.
These successes have been achieved in a perturbative framework, and are necessarily qualitative at best, since non-perturbative phenomena are essential to an understanding of supersymmetry breaking and other important matters of detail.
The subject of string theory arose in the late 1960's in an attempt to describe strong nuclear forces. This approach to the description of strong nuclear forces was a quite active subject for about five years, until it was abandoned because it ran into various theoretical difficulties and because a better theory came along.
There were two main problems that stymied us in our attempts to use string theory to describe the strong nuclear forces. One was that the theory required the existence of a kind of particle that we didn't want -- namely a particle with no mass and two units of spin. Its existence was very generic and very frustrating. The second problem was that the theory required that space-time have ten dimensions (nine space and one time), whereas the correct answer is clearly four (three space and one time).
As if all that weren't bad enough, around 1973 quantum chromodynamics (QCD) -- the SU(3) part of the standard model -- merged as a convincing theory of the strong nuclear force.
One curious fact about string theory in the 1968--1973 period is that it took two years studying various complicated mathematical formulas before several people realized that these were formulas describing the interactions of extended one-dimensional objects, which were named ``strings.'' Once this was realized, it became clear that this type of theory was outside the framework of conventional quantum field theory, which as we have emphasized, is based on point-like elementary particles.
Another important development during this period (in 1971) was the discovery that to incorporate a class of elementary particles called fermions (electrons and quarks are examples) string theory requires a two-dimensional version of supersymmetry. This led to the development of space-time supersymmetry, which was eventually recognized to be a generic feature of all consistent string theories (hence the name superstrings").
I have touched on some of the highlights of the current revolution, but there is much more that does not fit here. For example, I have not discussed the dramatic discoveries of Seiberg and Witten for supersymmetric gauge theories and their extensions to string theory. Another important development due to Vafa (called F theory) has made it possible to construct large new classes of non-perturbative vacua of Type IIB superstrings.
Despite all the progress that has taken place in our understanding of superstring theory, there are many important questions whose answers are still unknown. It is not clear how many important discoveries still remain to be made before it will be possible to answer the ultimate question that we are striving towards -- why does the universe behave the way it does?
Short of that, we have some other pretty big questions. What is the best way to formulate the theory? How and why is supersymmetry broken? Why is the cosmological constant, which characterizes the energy density of the vacuum, so small (or zero)? How is a realistic solution of the theory chosen from the myriad of possibilities? What are the cosmological implications of the theory? What testable predictions can we make?
The basic scale of those first string theories is discribed below.
|
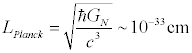
Scale of Strings.
PhysLINK.com - The Ultimate Physics & Astronomy Reference & Education Online Source |